1_mushroom
·
Edwin.Liang
数据来源
数据来自kaggle Mushroom Dataset ,kaggle的数据来自这里,通过蘑菇的伞帽直径、伞帽形状、伞帽颜色等信息判断蘑菇是否有毒
下表展示前五行数据,其中class列表示蘑菇是否有毒:
| cap-diameter | cap-shape | gill-attachment | gill-color | stem-height | stem-width | stem-color | season | class |
|---|---|---|---|---|---|---|---|---|
| 1372 | 2 | 2 | 10 | 3.8074667544799388 | 1545 | 11 | 1.8042727086281731 | 1 |
| 1461 | 2 | 2 | 10 | 3.8074667544799388 | 1557 | 11 | 1.8042727086281731 | 1 |
| 1371 | 2 | 2 | 10 | 3.6124962945838073 | 1566 | 11 | 1.8042727086281731 | 1 |
| 1261 | 6 | 2 | 10 | 3.7875718095925786 | 1566 | 11 | 1.8042727086281731 | 1 |
| 1305 | 6 | 2 | 10 | 3.711971019020609 | 1464 | 11 | 0.9431945538974952 | 1 |
数据分析
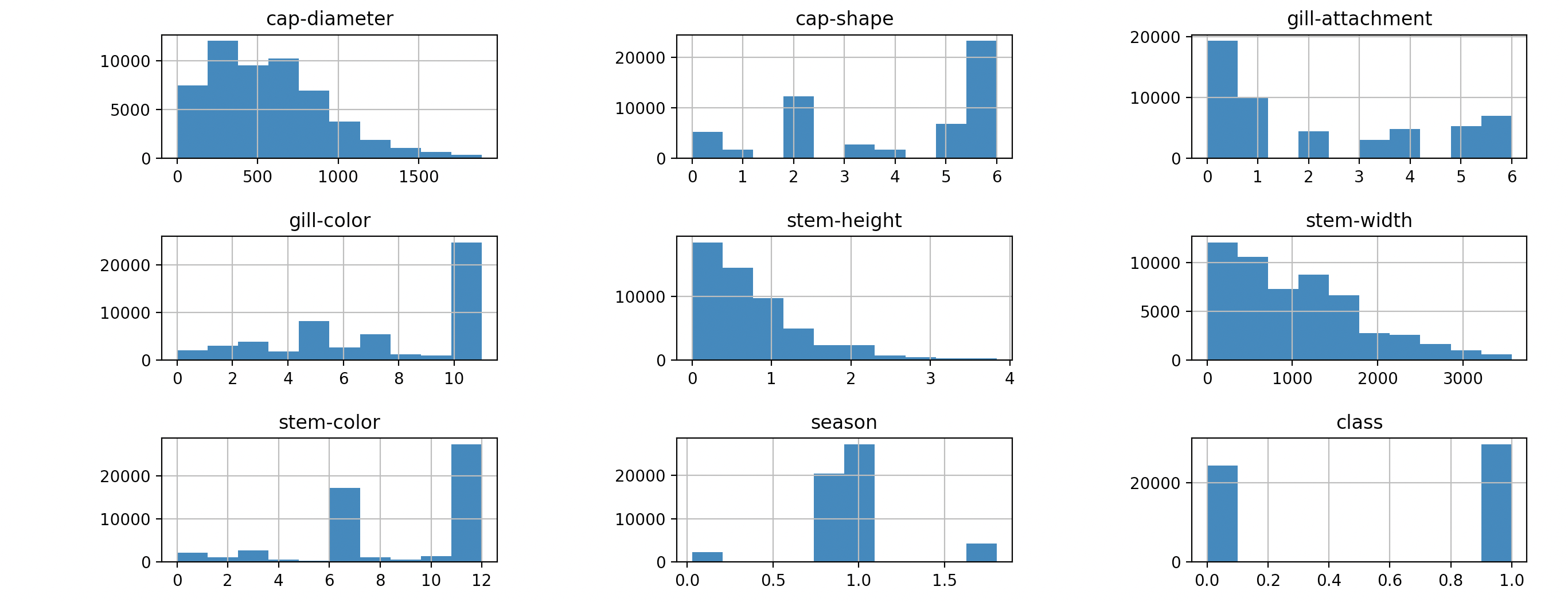
数据直方图
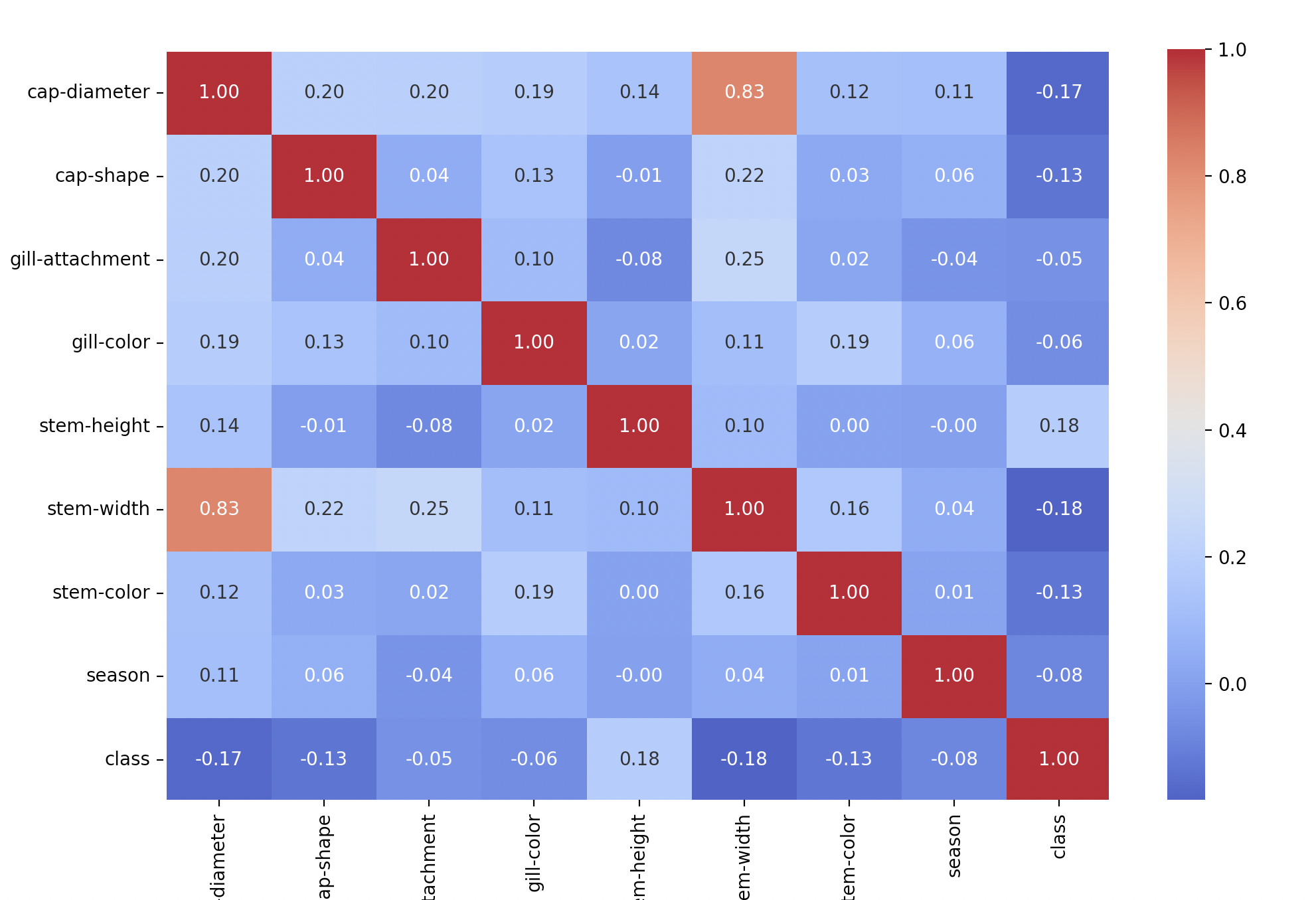
相关性分析
三维效果展示
展示$stem-width、stem-height、cap-diameter$三种特征与结果$class$之间的关系

20240515
特征工程
经过检查,来自kaggle的数据没有缺失项,同时未发现明显离群数据,是已经经过清洗之后的结果。依据相关性分析的结论,简单粗暴的将特征分为三个等级
- $level1$:相关性最高,包含三个特征$cap-diameter、stem-height、stem-width$
- $level2$:相关性次高,包含两个特征$cap-shape、stem-color$
- $level3$:低相关性,包含三个特征$gill-attachment、gill-color、season$
对上述所有特征做$min-max$归一化处理,并将$level1$归一化结果放大100倍、$level2$结果放大10倍,$level3$保持不变
模型确定
-
模型:选择比较简单的全连接网络作为本次测试模型
-
优化器:选择$SGD$优化器
-
损失函数:选择二值分类问题中比较常用的$CrossEntropyLoss$函数
完整代码
import sys
sys.path.append('/Users/kureisersen/Documents/python3/ai/')
from SOURCE import *
def getData():
class mushroomData(Dataset):
def __init__(self):
data = pd.read_csv("/Users/kureisersen/Documents/python3/ai/data/dateDir/mushroom_cleaned.csv")
level1 = ["cap-diameter","stem-height","stem-width"]
level2 = ["cap-shape","stem-color"]
level3 = ["gill-attachment","gill-color","season"]
# value_to_scaler = ["cap-diameter","cap-shape","gill-attachment","gill-color","stem-height","stem-width","stem-color","season"]
for i in level1:
data[i] = df_min_max(data[i],0,100)
for i in level2:
data[i] = df_min_max(data[i],0,10)
for i in level3:
data[i] = df_min_max(data[i],0,1)
self.file_data = data
def __len__(self):
return self.file_data.shape[0]
def __getitem__(self, idx):
self.file_data.iloc[idx]
return torch.tensor(self.file_data.iloc[[idx],[0,1,2,3,4,5,6,7]].values[0],dtype=torch.float32), torch.tensor(self.file_data.iloc[[idx],[8]].values[0],dtype=torch.long)
return mushroomData()
def splitData(dataset):
train_dataset, val_dataset = random_split(dataset, [0.025, 0.975])
return train_dataset,val_dataset
def createNet(n_input,n_hidden,n_output):
class Net(torch.nn.Module):
def __init__(self,n_input,n_hidden,n_output):
super(Net,self).__init__()
self.hidden1 = torch.nn.Linear(n_input,n_hidden)
self.hidden2 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden3 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden4 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden5 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden6 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden7 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden8 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden9 = torch.nn.Linear(n_hidden,n_output)
# self.hidden10 = torch.nn.Linear(n_hidden,n_hidden)
# self.hidden11 = torch.nn.Linear(n_hidden,n_output)
def forward(self, input):
out = self.hidden1(input)
out = torch.nn.functional.relu(out)
out = self.hidden2(out)
out = torch.nn.functional.relu(out)
out = self.hidden3(out)
out = torch.nn.functional.relu(out)
out = self.hidden4(out)
out = torch.nn.functional.relu(out)
out = self.hidden5(out)
out = torch.nn.functional.relu(out)
out = self.hidden6(out)
out = torch.nn.functional.relu(out)
out = self.hidden7(out)
out = torch.nn.functional.relu(out)
out = self.hidden8(out)
out = torch.nn.functional.relu(out)
out = self.hidden9(out)
out = torch.nn.functional.relu(out)
# out = self.hidden10(out)
# out = torch.nn.functional.relu(out)
# out = self.hidden11(out)
# out = torch.nn.functional.relu(out)
return out
return Net(n_input,n_hidden,n_output)
if __name__ == '__main__':
dataset = getData()
train_dataset, val_dataset = splitData(dataset)
BATCH_SIZE = 8
train_loader = DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True,drop_last=True)
valid_loader = DataLoader(dataset=val_dataset, batch_size=BATCH_SIZE)
net = createNet(8,10,2)
lossFun = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
for i in range(2000):
loss_sum = 0
accuracy = 0
print('--------第{}轮--------'.format(i))
for idx,(data,lable) in enumerate(train_loader):
y_pred = net(data)
lable = torch.reshape(lable,(1,BATCH_SIZE))[0]
loss = lossFun(y_pred,lable)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_sum += loss.item()
accuracy += (y_pred.argmax(1)==lable).sum()/BATCH_SIZE
print('第{}轮--平均loss值{}--平均正确率{}'.format(i,loss_sum/len(train_loader),accuracy/len(train_loader)))
训练结果
目前测得最好成绩是正确率70%😂,还在优化中
20240520
特征工程
沿用$20240515$版本对数据特征的处理方法,所不同的是,将$level1、level2$归一化结果放大10倍,$level3$保持不变
模型确定
-
模型:依旧选择全连接网络作为本次测试模型,模型层数确定为8层,同时最后一层的输出不再经过$RELU$激活函数,同时$BATCHSIZE$调整为128增加模型泛化能力
-
优化器:选择$Adadelta$优化器,上个版本的$SGD$优化器loss下降速度慢,在调整$lr$的过程中尝试了一下动态学习率,比较余弦退火、手动控制$SGD$学习率等方式,发现$Adadelta$优化器在下降速度以及$loss$值变化的稳定性上都有较好的表现
-
损失函数:选择$CrossEntropyLoss$函数
完整代码
import sys
sys.path.append('/Users/kureisersen/Documents/python3/ai/')
from SOURCE import *
def getLrInFile():
fo = open("/Users/kureisersen/Documents/python3/ai/train/lr.txt","r")
code = fo.read()
fo.close()
return float(code)
def adjust_learning_rate(optimizer, lr):
for param_group in optimizer.param_groups:
param_group['lr'] = lr
def getData():
class mushroomData(Dataset):
def __init__(self):
data = pd.read_csv("/Users/kureisersen/Documents/python3/ai/data/dateDir/mushroom_cleaned.csv")
level1 = ["cap-diameter","stem-height","stem-width"]
level2 = ["cap-shape","stem-color"]
level3 = ["gill-attachment","gill-color","season"]
# value_to_scaler = ["cap-diameter","cap-shape","gill-attachment","gill-color","stem-height","stem-width","stem-color","season"]
for i in level1:
data[i] = df_min_max(data[i],0,10)
for i in level2:
data[i] = df_min_max(data[i],0,10)
for i in level3:
data[i] = df_min_max(data[i],0,1)
self.file_data = data
def __len__(self):
return self.file_data.shape[0]
def __getitem__(self, idx):
self.file_data.iloc[idx]
return torch.tensor(self.file_data.iloc[[idx],[0,1,2,3,4,5,6,7]].values[0],dtype=torch.float32), torch.tensor(self.file_data.iloc[[idx],[8]].values[0],dtype=torch.long)
return mushroomData()
def splitData(dataset):
train_dataset, val_dataset = random_split(dataset, [0.8, 0.2])
return train_dataset,val_dataset
def createNet(n_input,n_hidden,n_output):
class Net(torch.nn.Module):
def __init__(self,n_input,n_hidden,n_output):
super(Net,self).__init__()
self.hidden1 = torch.nn.Linear(n_input,n_hidden)
self.hidden2 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden3 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden4 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden5 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden6 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden7 = torch.nn.Linear(n_hidden,n_hidden)
self.hidden8 = torch.nn.Linear(n_hidden,n_output)
# self.hidden9 = torch.nn.Linear(n_hidden,n_hidden)
# self.hidden10 = torch.nn.Linear(n_hidden,n_output)
def forward(self, input):
out = self.hidden1(input)
out = torch.nn.functional.relu(out)
out = self.hidden2(out)
out = torch.nn.functional.relu(out)
out = self.hidden3(out)
out = torch.nn.functional.relu(out)
out = self.hidden4(out)
out = torch.nn.functional.relu(out)
out = self.hidden5(out)
out = torch.nn.functional.relu(out)
out = self.hidden6(out)
out = torch.nn.functional.relu(out)
out = self.hidden7(out)
out = torch.nn.functional.relu(out)
out = self.hidden8(out)
# out = torch.nn.functional.relu(out)
# out = self.hidden9(out)
# out = torch.nn.functional.relu(out)
# out = self.hidden10(out)
# out = torch.nn.functional.relu(out)
return out
return Net(n_input,n_hidden,n_output)
if __name__ == '__main__':
dataset = getData()
train_dataset, val_dataset = splitData(dataset)
BATCH_SIZE = 128
train_loader = DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True,drop_last=True)
valid_loader = DataLoader(dataset=val_dataset, batch_size=BATCH_SIZE,drop_last=True)
net = createNet(8,20,2)
lossFun = torch.nn.CrossEntropyLoss()
# optimizer = torch.optim.SGD(net.parameters(), lr=getLrInFile())
optimizer = torch.optim.Adadelta(net.parameters())
# CosineLR = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=20, eta_min=0)
for i in range(2000):
loss_sum = 0
accuracy = 0
print('----------------------------第{}轮----------------------------'.format(i))
for idx,(data,lable) in enumerate(train_loader):
y_pred = net(data)
lable = torch.reshape(lable,(1,BATCH_SIZE))[0]
loss = lossFun(y_pred,lable)
optimizer.zero_grad()
loss.backward()
# CosineLR.step()
# adjust_learning_rate(optimizer, getLrInFile())
optimizer.step()
loss_sum += loss.item()
accuracy += (y_pred.argmax(1)==lable).sum()/BATCH_SIZE
valid_loss_sum = 0
valid_accuracy = 0
with torch.no_grad():
for idx,(data,lable) in enumerate(valid_loader):
y_pred = net(data)
lable = torch.reshape(lable,(1,BATCH_SIZE))[0]
loss = lossFun(y_pred,lable)
valid_loss_sum += loss.item()
valid_accuracy += (y_pred.argmax(1)==lable).sum()/BATCH_SIZE
print('第{}轮--平均loss值{}--平均正确率{}--验证集loss值{}--验证集平均正确率{}'.format(i,loss_sum/len(train_loader),accuracy/len(train_loader),valid_loss_sum/len(valid_loader),valid_accuracy/len(valid_loader)))
训练结果
模型在训练集中的正确率稳定在98%,在测试集中的正确率稳定在97%,
